algo:start
This is an old revision of the document!
Algorithme
Le cœur de Triskele est un algorithme de construction d'arbre en complexité linéaire.
Pour maintenir une complexité linaire Triskele utilise le tri comptage
La construction d'un arbre utilise l'algorithme dérivé d'union-find
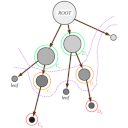
Schématiquement, tout les pixels font référence à un nœud et les nœuds font référence à un nœud (sauf la racine).
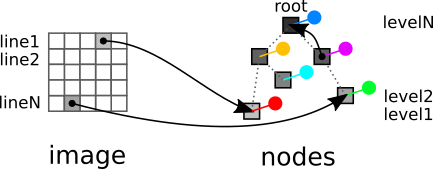
Représentation sous la forme de tableaux
- le tableau des parents (pixels et nœuds)
- les tableau des attributs (nœuds)
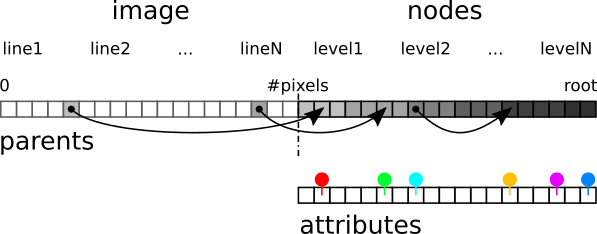
Présentation de l'Algorithmes de construction d’un arbre :
Nous allons expliquer le fonctionnement de l'Algorithmes de construction d’un arbre par un exemple, en détaillant les différentes étapes.
| Étape actuelle | Explication du fonctionnement de l'étape en détails |
|---|---|
| Comme exemple, nous allons prendre un tableau (dans le côté gauche de l'image) de dimensions 4×4, chaque case correspond à la valeur numérique d’un pixel Le tableau weights contiendras les poids des couples de pixels, leur pondération Le tableau parents correspondras au liens entre chaque couple de pixels, les noeuds de l'arbre Le tableau child-count compteras le nombre d'enfant reliés à un noeud |
|
 | Comme expliqué dans le résumé, l’algorithme va balayer de façon linéaire l’image afin de créer des couples de pixels pour chaque pixel présent dans l’image Donc l’algorithme crée des couples de pixels A et B, et leur attribut leurs pondération (ici appelé W) qui correspond à leurs poids, la valeur la plus grande entre les deux pixels, ce poids correspond à la valeur d'obscurité du couple de pixels. Un fois tout les couples crées, ils sont triés par leur pondération, par ordre croissant, ce tableau sera utilisé pour créer l'arbre, |
 | Nous passons maintenant à la création de l'arbre, de façon linéaire, à commencer par la création du premier parent, puis du premier noeud. Pour ce premier parent, on sélectionne le premier couple de pixels du tableau (ici représenté en rouge) en l'ajoutant dans le tableau parents Ce premier parent correspond naturellement au couple de pixels avec le poids le plus faible (tableau triés par ordre décroissant) Sa position a - b est en 6 - 7 Le tableau short-cut permet de désigner le leader lors des étapes pour gagner du temps d'exécution La valeur du tableau child-count de la premiere case correspond au nombre de couple de pixel enfant appartenant au parent (ici pour l'instant 2) |
 | Pour la suite de la construction de l'arbre, on sélectionne le couple de pixel suivant dans le tableau trié, ici de valeur de pondération 3 représenté en jaune. On rajoute une case parents dans le tableau parents. Comme un pixel du couple de pixel actuelle appartient aussi au couple de pixel précédent, on raccorde le couple avec le couple précédent en créant un noeud. On peut remarquer que dans la première case du tableau parents, on intègre une case jaune pour représenter la liaison du noeud entre les deux couples. Le noeud n'est plus jamais remis en question. On peut avancer dans la liste. Dans tableau short-cut on peut relever les liaisons entre les pixels utilisé qui désigne le leader (en position 10) |
 | Pour le troisième couple, Comme un pixel du couple de pixel actuel appartient aussi au couple de pixel précédent (le pixel en position 7), on raccorde le couple avec le couple précédent en créant un noeud. On peut remarquer que dans le tableau parent, le parent vert a été relié au parent jaune Comme pour chaque parent créé : - On ajoute le poid du couple dans le tableau weights - On ajoute le nombre d'enfant raccordé au parent dans le tableau child-count - Le short-cut désigne le leader - A la position du leader on insère la valeur correspondant au placement du noeud dans l'arbre (2éme tableau) |
 | Pour le quatrième couple, aucun des deux pixels n'a déjà été ajoutés à l'arbre, on ajoute donc le parent au tableau parents en créant un noeud sans le raccorder a un autre parent. On créé ici une autre branche. Comme pour chaque parent créé : - On ajoute le poid du couple dans le tableau weights - On ajoute le nombre d'enfant raccordé au parent dans le tableau child-count - Le short-cut désigne le leader - A la position du leader on insère la valeur correspondant au placement du noeud dans l'arbre (2éme tableau) |
 | Pour le cinquiéme couple, un des pixels est déjà utilisé par le parent 3 (vert), on ne crée pas de parent car la branche actuelle n'est pas reliée à l'arbre, on ajoute simplement le pixel qui n'est pas déjà utilisé, au parent 3, on incrément donc la valeur child-count de 1 (voir 4eme case du tableau child-count) |
 | Pour le cinquième couple, |
 | On construit ainsi l'arbre |
 | |
 | |
 |
algo/start.1624397262.txt.gz · Last modified: by antoine