min-max-tree:start
Differences
This shows you the differences between two versions of the page.
| Both sides previous revisionPrevious revisionNext revision | Previous revision | ||
| min-max-tree:start [2022/06/15 05:10] – modification externe 127.0.0.1 | min-max-tree:start [2022/11/22 14:32] (current) – charles | ||
|---|---|---|---|
| Line 5: | Line 5: | ||
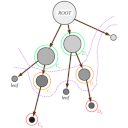
| {{: | {{: | ||
| - | Dans cet exemple, nous allons construire une représentation hiérarchique de l' | + | Dans cet exemple, nous allons construire une représentation hiérarchique de l' |
| Pour bien comprendre la notion d' | Pour bien comprendre la notion d' | ||
| Line 20: | Line 20: | ||
| {{: | {{: | ||
| - | En appliquant un filtre (élagage) pour les nœuds de taille | + | En appliquant un filtre (élagage) pour les nœuds de taille |
| Celle du dessous (qui n'est pas encadrée) est l' | Celle du dessous (qui n'est pas encadrée) est l' | ||
| - | {{: | + | {{: |
| Les commandes pour obtenir ces résultats sont | Les commandes pour obtenir ces résultats sont | ||
| <code bash> | <code bash> | ||
| Line 44: | Line 43: | ||
| ====== Exemple de Min-Tree ====== | ====== Exemple de Min-Tree ====== | ||
| - | Nous venons de présenter un arbre MAX, dont les feuilles portent les valeurs | + | Nous venons de présenter un arbre MAX, dont les feuilles portent les valeurs |
| Cette fois, il s'agit d' | Cette fois, il s'agit d' | ||
| Line 59: | Line 58: | ||
| {{: | {{: | ||
| - | En appliquant un filtre (élagage) pour les nœuds de taille | + | En appliquant un filtre (élagage) pour les nœuds de taille |
| Celle du dessous (qui n'est pas encadrée) est l' | Celle du dessous (qui n'est pas encadrée) est l' | ||
min-max-tree/start.1655269852.txt.gz · Last modified: by 127.0.0.1