Pour illustrer l'utilisation de Triskele nous allons partir de l'extrait d'une image satellite située au bout de la piste 05 (nord est) de l'aéroport international de Strasbourg. Le sud de l'image représente le rond-point entre la M400 et la M392. Le sud-est représente l'aéroparc 4.

Dans cet exemple, nous allons construire une représentation hiérarchique de l'image. Plus précisément un arbre d'inclusion où chaque nœud de l'arbre contient des nœuds ou des pixels suivant une règle. Dans notre cas, nous avons choisi un arbre dit MAX, car les feuilles contiennent les valeurs maximales. On donnera au nœud la valeur minimale de tous ses fils. Dans ce cas, tous les fils auront une valeur supérieure ou égal à leur père. Si l'on manipule une image en niveau de gris sur un octet (entre 0 et 255), la racine pourra avoir la valeur 0 et les feuilles 255. Le parcours d'une branche entre la racine et une feuille donnera une fonction monotone croissante.

Pour bien comprendre la notion d'inclusion, on peut imaginer des couches empilées de valeur la plus foncée (0) à la valeur la plus claire. A chaque couche, on découpe un masque qui correspond à ce qu'il faut ajouter de valeur plus claire pour se rapprocher du résultat final.

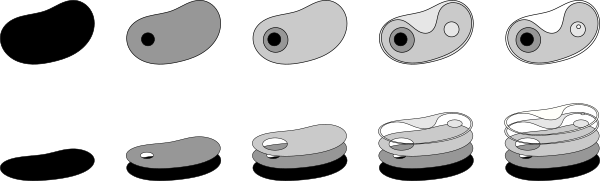
Une fois que nous disposons de ces couches, une représentation hiérarchique revient à relier un élément d'une couche (un nœud) avec les éléments qui se trouvent superposés sur lui.

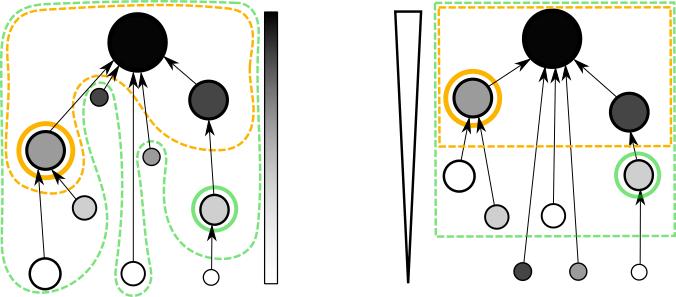
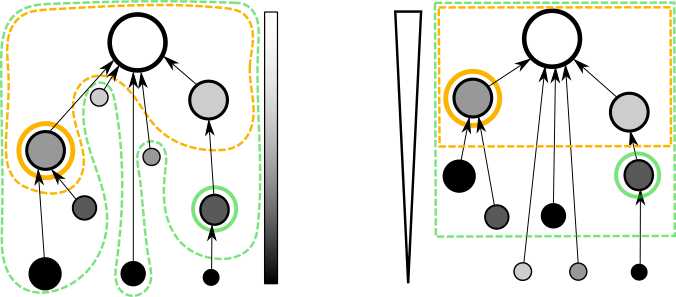
Les informaticiens ont l'habitude de représenter la racine en haut et les feuilles en bas. Dans l'exemple ci-dessous, la racine (qui représente toute l'image) est en haut. Dans la partie gauche du schéma, nous avons relié les nœuds en les plaçant sur leur niveau de gris respectif. Évidemment, rien ne lie la taille des nœuds (leur nombre de pixels) à leur niveau de gris. La seule chose que l'on sait, c'est que la racine est la valeur la minimum et que sa taille est la plus grande.

Nous voulons réaliser des opérations sur cet arbre, comme élaguer les branches les plus petites (traits en pointillés). Dans ce cas, il est plus facile de disposer sur le schéma les nœuds en fonction de leur taille (partie droite du schéma).

En appliquant un filtre (élagage) pour les nœuds de taille inférieur à 100 (ligne verte) et 1000 pixels (ligne orange) et en reconstruisant des images suivant un processus inverse, on obtient 3 images ci-dessous.

Celle du dessous (qui n'est pas encadrée) est l'image d'origine. Dans celle qui est encadrée en vert pointillé, les petits objets clairs ont disparu (le cercle vert montre la disparition de voitures sur un parking). Dans celle qui est encadrée en orange pointillée, les moyens objets ont disparu (le cercle orange montre la disparition des détails de la toiture de l'aéroparc 4).

Les commandes pour obtenir ces résultats sont

channelGenerator strasbourg.tif max-100.tif -b 0 -t MAX --thresholds 100
channelGenerator strasbuorg.tif max-1000.tif -b 0 -t MAX --thresholds 100

Il est possible de profiter de la particularité de l'encodage des images couleurs en rouge-vert-bleu des ordinateurs pour mettre en avant les différences entre les résultats. On utilisera la commande

channelGenerator strasbourg.tif max-0-100-1000.tif -c 0 -b 0 -t MAX --thresholds 100,1000

Dans ce cas les éléments clairs seulement présent dans la première couche (moins de 100 pixels) seront en rouge. Ceux présents dans les 2 premières (moins de 1000 pixels seront en orange (rouge et vert)).

Nous venons de présenter un arbre MAX, dont les feuilles portent les valeurs maximums de l'image. Nous pouvons avoir la démarche symétrique : un arbre MIN possède des feuilles qui portent les valeurs minimums.

Cette fois, il s'agit d'imaginer des couches empilées de valeur la plus claire (la plus élevée) à la valeur la plus foncée (0). A chaque couche, on découpe un masque qui correspond à ce qu'il faut ajouter de valeur plus sombre pour se rapprocher du résultat final.

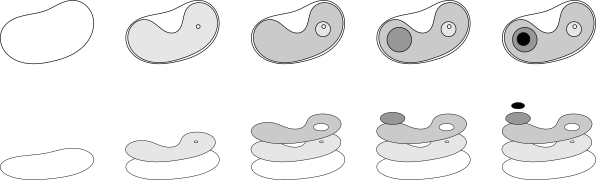
Une fois que nous disposons de ces couches, une représentation hiérarchique revient à relier un élément d'une couche (un nœud) avec les éléments qui se trouvent superposés sur lui.

En procédant de la même manière que précédemment, la racine (qui représente toute l'image) est en haut. Dans la partie gauche du schéma, nous avons relié les nœuds en les plaçant sur leur niveau de gris respectif. De nouveau, rien ne lie la taille des nœuds (leur nombre de pixels) à leur niveau de gris. La seule chose que l'on sait, c'est que la racine est la valeur la minimum et que sa taille est la plus grande.

Dans ce cas, l'élagage des branches les plus petites (traits en pointillés) va retirer des éléments les plus sombres. Pour mieux visualiser l'opération, nous disposons sur le schéma les nœuds en fonction de leur taille (partie droite du schéma).

En appliquant un filtre (élagage) pour les nœuds de taille inférieure à 10 (ligne verte) et 10000 pixels (ligne orange) et en reconstruisant des images suivant un processus inverse, on obtient 3 images ci-dessous.

Celle du dessous (qui n'est pas encadrée) est l'image d'origine. Dans celle qui est encadrée en vert pointillé, les petits objets sombres ont disparu (le cercle vert montre la disparition de l'ombre des voitures sur un parking). Dans celle qui est encadrée en orange pointillée, les moyens objets ont disparu (le cercle orange montre la disparition de l'ombre du pont sur le rond-point).

Les commandes pour obtenir ces résultats sont

channelGenerator strasbourg.tif min-10.tif -b 0 -t MIN --thresholds 10
channelGenerator strasbuorg.tif min-10000.tif -b 0 -t MIN --thresholds 10000

On peut compiler les couches pour une visualisation en fausses couleurs et faire ressortir en vert (seul le rouge reste sombre) de petits objets et en bleu (le rouge et le vert reste sombre) des objets de moyenne taille. On utilisera la commande

channelGenerator strasbourg.tif min-0-10-10000.tif -c 0 -b 0 -t MIN --thresholds 10,10000